MEX関数応用その２....................................................................................................... 63

Hough変換とは？........................................................................................................ 63

Hough変換のアルゴリズム.......................................................................................... 63

実際のHough変換のインプリメンテーション............................................................. 64

MEX関数によるHough変換アルゴリズムのインプリメント...................................... 65

1.サイン・コサインテーブルの作成.......................................................................... 65

2. find関数による二値化.......................................................................................... 65

3.hough変換処理..................................................................................................... 66

4.処理データの配列処理............................................................................................ 66

MEX関数　高速化のためのテクニック........................................................................ 68

Hough変換の使用例.................................................................................................... 70

Hough変換サンプル例その1................................................................................... 70

Hough変換サンプル例その2................................................................................... 63

量子化誤差の影響の軽減............................................................................................... 63

高速化のためのファインチューニング.......................................................................... 64

Sparse行列、Uint8行列への対応................................................................................ 65

演習問題........................................................................................................................... 68

 

 

MEX関数応用その２

　近年、コンピュータ処理能力の向上により、リアルタイムへの応用が不可能であったような計算処理が現実に出来るような環境になりつつある。このような処理の一つとしてHough変換がある。ここでは、Hough変換を例に、処理速度アップの効果的な例としてMEX関数化とその速度の最適化を順を追って説明していく。

Hough変換とは？

　Hough変換とは、投票メカニズム（voting）を使った曲線パラメータ推定アルゴリズムである。ある種の積分操作をベースにしたアルゴリズムのため、一般的に使用されている微分操作をベースにしたエッジ検出、グルーピングなどのテクニックと比較してノイズを強調するようなことはない。そのためノイズに対しても強く比較的実用的なアルゴリズムの一つであると言える。Hough変換では、いくつかの組み合わせのパラメータにより与えられる曲線上に存在する点座標を投票する。では、簡単で一般的である2つのパラメータである直線にフィットするHough変換について考えてみよう。直線の式を

 　　　　　　　　　　　　　　　　　(1)

とする。この式では、x,yは、2値化された画像中の点座標、m,cは、それぞれ傾き、切片パラメータを表す。今、上の式についてm,cを変数、x,yを定数であると考えてみよう。

 　　　　　　　　　　　　　　　　　(2)

この式は、m-c座標系において直線を表すことになる。傾きと切片がx,yにより決定される。つまり点(x,y)は、m-c平面における直線の一部に対応することになる。m-c座標系では、傾きが0になった時、問題になる。そのため実用的にHough変換は、極座標現

　　　　　　　　　　　　　　　　(3)

が使われる。この場合、観測点(x,y)は、座標空間にマッピングされる。直線の場合、もし複数点nが同じ観測座標x-yの直線上にあった場合、それらに対応する同じポイントをさすことになる。このことを利用し、空間にマスを作り対応する点に対し投票する。最も投票の大きい個所、つまりもっともマッチングする個所がもっともマッチした直線を意味する。

 

Hough変換のアルゴリズム

 

l         適当にパラメータ空間の量子化する。

l         それぞれのパラメータ空間におけるセルを加算できるユニットと仮定する。すべてのセルを0に初期化する。

l         画像空間において2値化したそれぞれの(x,y）ポイントに対応するパラメータ空間のセルに1を加える。

l         加算されたセルの最大値がパラメータモデルの最も特徴となるパラメータになる。

 

　この手順がHough変換と言われる。ここでのパラメータ空間は離散的な配列を仮定している。先の説明では、直線を例に扱かった。特徴となるパラメータは、パラメータ空間の中の最大値で表現できる。またこの方法は、直線だけでなく円、曲線などにも適用可能である。Hough変換は、エッジ点におけるつながりやグルーピングなどのテクニックを要求しない。多少のノイズがある場合でも直線検出が可能である特徴を持つ。Hough変換の前提にあるものは、現存する大きなイメージ中の最もフィットするカーブ（直線）を見つけることである。パラメータ空間の中のピークが1つ以上ある場合には、その重心となる個所が推定パラメータになる。いくつかのカーブ（直線）のイメージが一致した場合には、パラメータ空間においていくつかのピークが出来る。この点を利用し、おのおののピークから、カーブ（直線）を検出することも可能である。この場合、どの程度の投票の大きさまでを直線またはノイズとみなすかが問題となる。

　もうひとつのHough変換の問題は、推定するパラメータの解像度は、離散パラメータ空間の大きさに関係している点である。解像度を高くしたい場合には、それなりのメモリ空間と処理時間が要求される。

また、Hough変換を直線でなく、カーブに円を適用する場合、パラメータは３次元になる。当然のことながら推定するパラメータ空間の次元が増えると、処理時間、メモリ空間とも指数的に必要になる。そのためHough変換は、多パラメータモデルに対しては、計算量が非常に多くなるため一般的には、あまり実用的はなくなってしまう。これら高速化の手法に関しては、様々な手法が論文として提案されているので各自探してもらいたい。

 

実際のHough変換のインプリメンテーション

 

では、実際MATLABでのhough変換のインプリメンテーションを見てみよう。このインプリメンテーションは、MATLABサイト(http://www.mathworks.com)のuser contributed Libraryの中のDimitrios Ioannou 氏の作成したhough.mのコメントの部分を削除しエッセンスの部分のみを表示したものである。

function res=hough(im,rhomax,thetamax)

[X,Y]=size(im);

if X~=Y,return;

elseif rem(X,2)==1,  return

end

d_rho=X/rhomax;

d_theta=pi/thetamax;

theta=0:d_theta:pi-d_theta;

smat=sin(theta);

cmat=cos(theta);

 [x,y]=find(im);

% translation by a pixel so that low left pixel has (0,0)

x=x-1;

y=y-1;

h1=((y-Y/2) * smat + (x-X/2) * cmat )/d_rho;

h2=h1+rhomax/2;

h3=round(h2);

res=zeros(rhomax,thetamax);

for j=0:rhomax-1

res(j+1,:)=sum(h3==j);

end

この関数では、入力されるイメージ行列は、偶数であり同じ大きさである必要がある。出力されるパラメータrho,thetaの解像度は、こちらで整数値を指定できる。この関数の処理は，大きく分けて

1.サイン・コサインテーブルの作成

2. find関数による二値化

3.hough変換処理

4.処理データの配列処理

の四つからなる。sin,cos関数は、比較的処理時間がかかる上、何回も参照されるため、あらかじめテーブルとして計算しておきそのテーブルの値を利用するようにしている。この方法は、C言語やMATLABなどでも適用できる高速化のテクニックの一つである。このスクリプトはMATLABの特性を考え、4の処理データの配列処理にあるfor文を除きほぼすべて処理でベクトル化し、高速化、簡潔な記述を実現している。

 

 

 

MEX関数によるHough変換アルゴリズムのインプリメント

 

では，この関数をMEX関数化してみよう．なおここで書かれたMEX関数は、一応C＋＋言語の機能も使っているため、コンパイルする場合には、拡張子.cppで保存する必要がある。

MEX関数では、

function res=hough(im,rhomax,thetamax)

の部分を変換すると

#include <stdio.h>

#include <math.h>

#include "mex.h"

void mexFunction(int nlhs,mxArray *plhs[],int nrhs,const mxArray *prhs[]) {

if ((nrhs != 3) || (nlhs != 1)) {

   mexPrintf("function res=hough(im,RHO_MAX,THETA_MAX)\n");

   mexPrintf("Translated from m file Copyright 1999 Gerox(c)%s\n",__DATE__);

   mexErrMsgTxt("\n");

}

int Y = (int)mxGetN(prhs[0]);

int X = (int)mxGetM(prhs[0]);

int rhomax = (int)mxGetScalar(prhs[1]);

int thetamax = (int)mxGetScalar(prhs[2]);

double *im = mxGetPr(prhs[0]);

plhs[0] = mxCreateDoubleMatrix(rhomax,thetamax,mxREAL);

}

となる．MATLABで実行するには，mexFunctionを使う．MEX関数か与えられる引数のポインタは，prhs,plhs配列の中に含まれ（それぞれ右辺，左辺を意味）る．nrhs,nlhsは，実行時の各引数の数を示している．MATLABでは，入出力の引数の数を実行時に指定することができる．引数のポインタから実際の値を取り出すには，mxGetScalar, mxGetPrなどの関数を用いる．

1.サイン・コサインテーブルの作成

theta=0:d_theta:pi-d_theta;

smat=sin(theta);

cmat=cos(theta);

MATLABでは，たったの三行で表現できるが，C言語で同等の表現をすると以下のようになる．

double *smat = (double*)mxCalloc(thetamax,sizeof(double));

double *cmat = (double*)mxCalloc(thetamax,sizeof(double));

   double tmp;

int i;

for (i = 0,tmp=0.0;i < thetamax;tmp += d_theta,i++) {

   smat[i] = sin(tmp);

   cmat[i] = cos(tmp);

}

SIN,COSテーブルの大きさは，実行時の解像度の指定の時に決まる．MEX関数の場合、配列の大きさを実行時に指定するには，mxCalloc関数により動的にメモリの確保をする必要がある。また，プログラムが終わるときは，必ずmxFree関数で確保したメモリを開放する必要がある。

2. find関数による二値化

[x,y]=find(im);

この命令では，im配列の中で０で無い座標をすべてx,yベクトルとして取り出せと言う命令である．この命令をC言語で書くと以下のようになる．

int f_length = 0;

for (i = 0;i < X * Y;i++) if(im[i] > 0) f_length++;

int *x = (int*)mxCalloc(f_length,sizeof(int));

int *y = (int*)mxCalloc(f_length,sizeof(int));

int count = 0;

for (i = 0;i < Y;i++) {

   for(j = 0;j < X;j++) {

    if(im[i * X + j] > 0) {

     x[count] = j;

     y[count] = i;

     count++;

    }

   }

}

MATLABでは配列の大きさは、実行時でもあらかじめ宣言すること無く変更することができるが、C言語ではそのようなことはできない。また、C言語で配列の大きさを実行時に宣言するには，ポインタを用い動的にメモリを確保する必要がある。そのため上のプログラムでは，まずfor文で配列imの要素の中で0より大きい数字が何個あるか調べている。その数がわかってから動的に確保した配列に値を代入している。

3.hough変換処理

h1=((y-Y/2) * smat + (x-X/2) * cmat )/d_rho;

h2=h1+rhomax/2;

h3=round(h2);

MATLABでは，全ての処理は，ベクトルでできるためたったの三行で終わってしまう。

1行目がHough変換のメインとなるところである。x,y座標とも中心が0となるようにオフセットX/2,Y/2を差分してから、sin,cosの計算しd_rhoで出力がrhoの最大値を超えないようにスケーリングしている。

2行目のh2は、配列のパラメータ化するための処理である。MATLABでの配列パラメータは、1より大きな値でなければならないためオフセットrhomax/2を加え全ての計算値が正の値になるようにしている。

int **h2;

h2 = (int**)mxCalloc(f_length,sizeof(int*));

for(i = 0;i < f_length;i++) h2[i] = (int*)mxCalloc(thetamax,sizeof(int));

   int rhomax_2=int(rhomax / 2.0);

for(i = 0;i < f_length;i++) {

   for(j = 0;j < thetamax;j++) {

    h2[i][j] = int((y[i] * smat[j] + x[i] * cmat[j]) + rhomax_2);

   }

}

まず，mxCalloc関数により二次元配列h2を動的に確保している。次にhough変換したデータをh2に代入している．ここでのh2は，実は，h3の処理をしているのだがC＋＋でのint関数（切り捨て）とMATLABのround関数（四捨五入）では，若干動作が異なるため，微妙に計算結果が異なる。（実用上ほとんど問題無いと思われるが．）

4.処理データの配列処理

for j=0:rhomax-1

res(j+1,:)=sum(h3==j);

end

ここでh3==j演算を行うと、h3行列と同じ大きさの行列が出力される。その行列の中身は、h3行列の要素の値がjである行列の要素の所を1に他の行列の要素を0となる行列が出力される。SUM関数の入力引数が行列の場合には、列要素ごとに合計が計算される。つまり、この場合、列要素の中で同じjとなる配列要素の数をカウントし合計しその結果をresへ代入している。C言語でこれと等価の処理を記述すると以下のようになる。

double *yy = mxGetPr(plhs[0]);

for (register int jjj = 0;jjj < rhomax;jjj++) {

   for (register int iii = 0;iii < thetamax;iii++) {

    for (register int k = 0; k < f_length;k++) {

     if(h2[k][iii] == jjj) yy[(int)(jjj+iii * rhomax)] += 1.0;

    }

   }

}

この処理がHough変換のメインとなる投票（voting）である。

以上の処理を踏めば良い．これをまとめたのが以下のプログラムである。

----------------- direct translated version------------------------------------------------------

#include <stdio.h>

#include <math.h>

#include "mex.h"

void mexFunction(int nlhs,mxArray *plhs[],int nrhs,const mxArray *prhs[]) {

if ((nrhs != 3) || (nlhs != 1)) {

   mexPrintf("function res=hough(im,RHO_MAX,THETA_MAX)\n");

   mexPrintf("Translated from m file Copyright 1999 Gerox(c)%s\n",__DATE__);

   mexErrMsgTxt("\n");

}

double rhomax,thetamax;

rhomax = mxGetScalar(prhs[1]);

thetamax = mxGetScalar(prhs[2]);

//[X,Y]=size(im);

int Y = (int)mxGetN(prhs[0]);

int X = (int)mxGetM(prhs[0]);

if (X != Y) {

   mexPrintf("Input image is not square. Exiting!\n");

   return;

} else {

   if ((X % 2) == 1) {

    mexPrintf("Input image size has to be even in pixels. Exiting!\n");

    return;

   }

}

double *im;

im = mxGetPr(prhs[0]);

double pi = 3.14159265358979;

// double d_rho=double(X)/ rhomax;

double d_theta=pi / thetamax;

// theta=0:d_theta:pi-d_theta;

double tmp;

int i,j;

//smat=sin(theta);

//cmat=cos(theta);

double *smat = (double*)mxCalloc(thetamax,sizeof(double));

double *cmat = (double*)mxCalloc(thetamax,sizeof(double));

double dd_rho = rhomax / double(X);

for (i = 0,tmp= 0.0;i < thetamax;tmp += d_theta,i++) {

   smat[i] = sin(tmp) * dd_rho;

   cmat[i] = cos(tmp) * dd_rho;

}

// [x,y]=find(im);

int f_length = 0;

for (i = 0;i < X * Y;i++) if(im[i] > 0) f_length++;

int *x = (int*)mxCalloc(f_length,sizeof(int));

int *y = (int*)mxCalloc(f_length,sizeof(int));

int count = 0;

for (i = 0;i < Y;i++) {

   for(j = 0;j < X;j++) {

    if(im[i * X + j] > 0) {

     x[count] = j - X/2;

     y[count] = i - Y/2;

     count++;

    }

   }

}

int **h2;

h2 = (int**)mxCalloc(f_length,sizeof(int*));

for(i = 0;i < f_length;i++) h2[i] = (int*)mxCalloc(thetamax,sizeof(int));

int rhomax_2=int(rhomax / 2.0);

for(i = 0;i < f_length;i++) {

   for(j = 0;j < thetamax;j++) {

    h2[i][j] = int((y[i] * smat[j] + x[i] * cmat[j]) + rhomax_2 + 0.5);

   }

}

plhs[0] = mxCreateDoubleMatrix((int)rhomax,(int)thetamax,mxREAL);

double *yy = mxGetPr(plhs[0]);

for (register int jjj = 0;jjj < rhomax;jjj++) {

   for (register int iii = 0;iii < thetamax;iii++) {

    for (register int k = 0; k < f_length;k++) {

     if(h2[k][iii] == jjj) yy[(int)(jjj+iii * rhomax)] += 1.0;

    }

   }

}

mxFree(smat);

mxFree(cmat);

mxFree(x);

mxFree(y);

for(i = 0;i < f_length;i++) mxFree(h2[i]);

mxFree(h2);

}

 素直にMATLABスクリプトをMEX関数化するだけで、処理速度が約50%の速くすることが出来る。（と言っても40秒が20秒になるだけだが．．．）一応、MEX関数にすることだけでも，高速化できるのであるがこれでもリアルタイム応用には、程遠い速さである。C言語の特性を生かし，チューニングする方法（register 宣言や、static 宣言など）も考えられるが，良くなっても20%程度のアップしかならない。

 

MEX関数　高速化のためのテクニック

　特に，このスクリプトを直接翻訳したHough変換関数の中を注意深く検討してみると、forループが多用されていることがわかる。MATLABでもそうであるが、C言語でもforループ内の処理は(何回も処理するので)時間がかかる。そのためループ内の処理を少し減らすだけでもかなり処理速度をアップすることができる．作ったMEX関数の部分を詳しく見てみよう。Hough変換のための2次元パラメータ空間配列を宣言し計算している個所がある。ここでの処理は、オフセットX/2,Y/2の引く操作をするために配列を宣言し計算している。Ｃ言語の場合、配列を動的に宣言するには、あらかじめその配列の数が分かっている必要がある。そのためまず該当する点が何点あるかf_lengthでカウントしチェックしている。

int f_length = 0;

for (i = 0;i < X * Y;i++) if(im[i] > 0) f_length++;

int *x = (int*)mxCalloc(f_length,sizeof(int));

int *y = (int*)mxCalloc(f_length,sizeof(int));

int count = 0;

for (i = 0;i < Y;i++) {

   for(j = 0;j < X;j++) {

    if(im[i * X + j] > 0) {

     x[count] = j - X/2;

     y[count] = i - Y/2;

     count++;

    }

   }

}

int **h2;

h2 = (int**)mxCalloc(f_length,sizeof(int*));

for(i = 0;i < f_length;i++) h2[i] = (int*)mxCalloc(thetamax,sizeof(int));

int rhomax_2=int(rhomax / 2.0);

for(i = 0;i < f_length;i++) {

   for(j = 0;j < thetamax;j++) {

    h2[i][j] = int((y[i] * smat[j] + x[i] * cmat[j]) + rhomax_2 + 0.5);

   }

}

カウントのためのループは、以下のように変更すると減らせる上にx,yの配列の確保が不要になる。

int f_length = 0;

for (i = 0;i < X * Y;i++) if(im[i] > 0) f_length++;

int **h2;

h2 = (int**)mxCalloc(f_length,sizeof(int*));

for(i = 0;i < f_length;i++) h2[i] = (int*)mxCalloc(thetamax,sizeof(int));

double rhomax_2=rhomax / 2.0;

int count = 0;

int Y_2 = Y/2;

int X_2 = X/2;

for (int ii = 0;ii < Y;ii++) {

   for(int jj = 0;jj < X;jj++) {

    if(im[ii * X + jj] > 0) {

     for(int k = 0;k < thetamax;k++) {

       h2[count][k] = (int)((ii - Y_2) * smat[k] + (jj - X_2) * cmat[k]+ rhomax_2 + 0.5);

     }

     count++;

    }

   }

}

plhs[0] = mxCreateDoubleMatrix((int)rhomax,(int)thetamax,mxREAL);

double *yy = mxGetPr(plhs[0]);

for (register int jjj = 0;jjj < rhomax;jjj++) {

   for (register int iii = 0;iii < thetamax;iii++) {

    for (register int k = 0; k < f_length;k++) {

     if(h2[k][iii] == jjj) yy[(int)(jjj+iii * rhomax)] += 1.0;

    }

   }

}

さらにもう一つ考えを進めてみよう。該当する点はf_lengthによりカウントされ、その数に合わせ2次元配列h2を動的に確保している。この計算では、h2行列の計算結果を元に更にループにより出力行列yyを計算している。実は、このh2の値の計算を最後のループに含めてしまうことで更にループの数を減らすことが出来る。

int rhomax_2=rhomax >> 1;

int Y_2 = Y >> 1;

int X_2 = X >> 1;

plhs[0] = mxCreateDoubleMatrix(rhomax,thetamax,mxREAL);

double *yy = mxGetPr(plhs[0]);

for (int ii = 0;ii < Y;ii++) {

   for(int jj = 0;jj < X;jj++) {

    if(im[ii* X + jj] > 0) {

     for(int k = 0;k < thetamax;k++) {

       int rho = (int)((ii-Y_2) * smat[k] + (jj-X_2) * cmat[k] + rhomax_2 + 0.5);

        if(rho < 0) continue;

        else {

         if(rho > X) continue;

         else yy[(int)(rho + k * rhomax)] += 1.0;

        }

     }

    }

   }

}

これのようにすると、ループ数を減らすことができる上，中間変数として使用していた動的配列x,y,h2などの確保もなくすことができる。この様に注意深くプログラミングすることで従来のMATLABのスクリプトと比較すると約100倍程度の速度アップもできる。

----------------- optimized for speed version------------------------------------------------------

#include <stdio.h>

#include <math.h>

#include "mex.h"

void mexFunction(int nlhs,mxArray *plhs[],int nrhs,const mxArray *prhs[]) {

if ((nrhs != 3) || (nlhs != 1)) {

   mexPrintf("function res=hough(im,RHO_MAX,THETA_MAX)\n");

   mexPrintf("Translated from m file Copyright 1999 Gerox(c)%s\n",__DATE__);

   mexErrMsgTxt("\n");

}

int rhomax,thetamax,X,Y;

rhomax = (int)mxGetScalar(prhs[1]);

thetamax = (int)mxGetScalar(prhs[2]);

//[X,Y]=size(im);

Y = (int)mxGetN(prhs[0]);

X = (int)mxGetM(prhs[0]);

if (X != Y) {

   mexPrintf("Input image is not square. Exiting!\n");

   return;

} else {

   if ((X % 2) == 1) {

    mexPrintf("Input image size has to be even in pixels. Exiting!\n");

    return;

   }

}

double *im;

im = mxGetPr(prhs[0]);

double pi = 3.14159265358979;

double d_theta=pi / (double)thetamax;

// theta=0:d_theta:pi-d_theta;

double *smat = (double*)mxCalloc(thetamax,sizeof(double));

double *cmat = (double*)mxCalloc(thetamax,sizeof(double));

double dd_rho = (double)rhomax / (double)X;

double tmp;

int i;

for (i = 0,tmp=0.0;i < thetamax;tmp += d_theta,i++) {

   smat[i] = sin(tmp) * dd_rho;

   cmat[i] = cos(tmp) * dd_rho;

}

// [x,y]=find(im);

int rhomax_2=rhomax >> 1;

int Y_2 = Y >> 1;

int X_2 = X >> 1;

plhs[0] = mxCreateDoubleMatrix(rhomax,thetamax,mxREAL);

double *yy = mxGetPr(plhs[0]);

for (register int ii = 0;ii < Y;ii++) {

   for(register int jj = 0;jj < X;jj++) {

    if(im[ii* X + jj] > 0) {

     for(register int k = 0;k < thetamax;k++) {

       register int rho = (int)((ii-Y_2) * smat[k] + (jj-X_2) * cmat[k])+ rhomax_2 + 0.5);

//      if((rho > -1) && (rho < X)) yy[(int)(rho + k * rhomax)] += 1.0;

        if(rho < 0) continue;

        else {

         if(rho > X) continue;

         else yy[(int)(rho + k * rhomax)] += 1.0;

        }

     }

    }

   }

}

mxFree(smat);

mxFree(cmat);

}

 

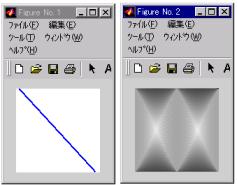
Hough変換の使用例

ここでの入力は、ペニーの丸い画像を2値化した画像である。50,50は、投票の際のメッシュの大きさを意味する。このインプリメンテーションでは、縦と横サイズは同じ画像でありかつデータ点数は偶数データのみしか処理できない。ここでは、円をhough変換により円を検出している。円の画像は、直線で近似するのは難しいが、Hough変換した画像の上部にうっすらとカーブ状にピークが出力されているのが確認できると思う。

使用例

close all

load penny

figure;imshow(P,[ ]);

data=P>200;

figure; imshow(data,[ ]);

result=houghf(data,50,50);

figure;imshow(result,[ ]);

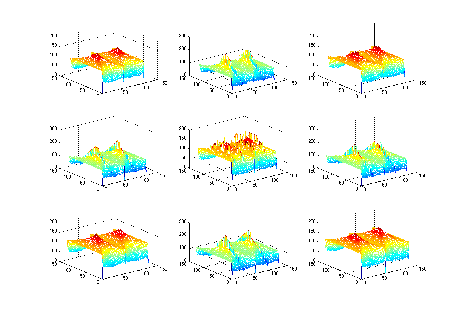
　　原画　　　　　　　　　　　　　2値化した画像　　　　　　　　Hough変換後

 

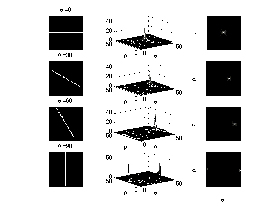
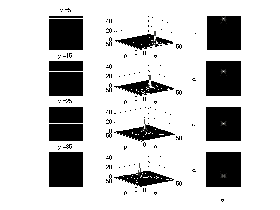
Hough変換サンプル例その1

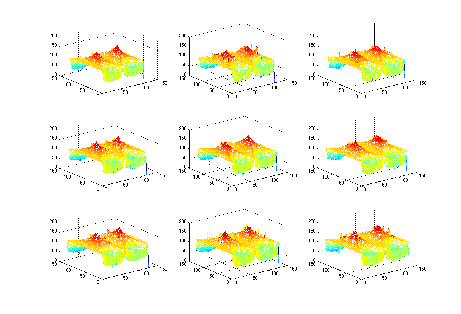
　実際にHough変換した例を示そう。上記のMEX関数(houghf.cpp)を応用したサンプルスクリプトを示す。ここでは、直線データを0度30度60度90度と回転させそれぞれhough変換をした図とy軸を5,15,25,35にずらして変換した図である。左側がオリジナルデータ真ん中が投票の結果、右側が最大値の変化を示している。この左側の図では、直線の角度のみが変化していることから最大値が左から右へ移動していく様子が見れる。右側の図では最大値が、上から下に下がっていく様子が見れる。

close all;

clear all

dataxy=[zeros(1,50);-25:24];

figure(1);count = 1;

for theta=[0 30 60 90]*pi/180

  rot = [cos(theta) sin(theta);-sin(theta) cos(theta)];

  ndata = round(rot*dataxy+25);

  allownums =find(((ndata(1,:)>0)+(ndata(2,:)>0)...

  +(ndata(1,:)<=50)+(ndata(2,:)<=50))==4);

  data = zeros(50,50);

  for i=allownums;data(ndata(1,i),ndata(2,i))=1;end

  subplot(4,3,count);count=count+1;

  imshow(data,[0 1]);

  title(['\theta =' num2str(theta*180/pi)]);

  subplot(4,3,count);count=count+1;

  hdata = houghf(data,50,50);

  mesh(hdata);

  xlabel('\theta');ylabel('\rho');

  subplot(4,3,count);count=count+1;

  imshow(hdata,[]);

  xlabel('\theta');ylabel('\rho');

end

figure(2);count = 1;

for y=[5 15 25 35]

  data = zeros(50,50);

  data(y,:)=1;

  subplot(4,3,count);count=count+1;

  imshow(data,[0 1]);

  title(['y =' num2str(y)]);

  subplot(4,3,count);count=count+1;

  hdata = houghf(data,50,50);

  mesh(hdata);

  xlabel('\theta');ylabel('\rho');

  subplot(4,3,count);count=count+1;

  imshow(hdata,[]);

  xlabel('\theta');ylabel('\rho');

end

また、この変換は、投票をベースにしているため多少のノイズが含まれた場合や、途切れた直線に対しても比較的安定に直線を検出することが出来る。

 

 

Hough変換サンプル例その2

　Hough変換の理解を深めるのに便利なマウスで空間座標をクリックするとそれに対応するx-y平面上で直線を表示するスクリプトを挙げておく。HandleGraphicsを駆使すると容易にこのようなデモンストレーションプログラムを作ることが出来る。この場合には、120x120のすべて1の行列をHough変換した例である。Figure1がx-y座標、Figure2がHough変換した座標系になっている。

close all;

bw=ones(120,120);

yy=min(size(bw));

bw=bw(1:yy,1:yy);

figure(1)

imshow(bw)

hold on;

hline1=plot(zeros(size(1:yy)),1:yy,'linewidth',2);

hold off

drawnow;

c=houghf(bw,yy,yy);

figure(2)

imshow(c,[]);axis square;

x=1:yy;

set(2,'windowbuttondown',['aaa=get(gca,''currentpoint'');',...

'theta = pi/(yy)*(aaa(1,1)-1);',...

'rho = (aaa(1,2)-1)-(yy)/2;',...

'y=(rho/sin(theta)-(x-(yy)/2)*cos(theta)/sin(theta))+(yy)/2;',...

'set(hline1,''Xdata'',y);',...

'drawnow;']);

set(1,'doublebuffer','on');

set(2,'doublebuffer','on');

 

xy座標　　　　　空間

 

量子化誤差の影響の軽減

　Hough変換は、投票によるパラメータ推定のため、求められるパラメータは、パラメータ空間の配列の区切り方と、直線の近似アルゴリズムによる。前のサンプルスクリプトの空間の図で気がついた人もいるかもしれないが、x-y座標空間と空間の点の分布は一様ではない。x-y座標空間のデータを全てhough変換すると2つのピークができる。これは、x-y行列では対角線（右、左斜めの直線）がもっとも長く引けるため投票の際カウントされやすいためである。また、実際何回か計算してみてわかったのであるが、hough変換するデータのサイズにより例えば、mesh(hough(ones(120,120),120,120));としてみると

となってしまう。これはある特定のthetaとrhoの所の感度が特に高くなっていることを意味する。ここで見ると、thetaがある特定の値30,90の時に明らかに大きな値が出ている。その周りはそれほど大きな値ではなく突然変化していることから、これは、パラメータ空間の区切り方とサインコサインテーブルの量子化誤差によるものであると考えられる。これは、sin,cosテーブルのスケーリングの際d_thetaの定義が十分ではなかったためであり、 double d_theta = pi / (double)thetamax ;

から

double d_theta = pi / (double)(thetamax - 1);

と変更すれば、若干は改善される。しかしこの変更は、あくまでsin,cosテーブルの補正のみで直線近似による量子化誤差は改善されない。そのため使用する場合には、一応、変換するデータの大きさからどの程度量子化誤差が生じるか調べていた方がよい。

一応、参考までに114点から130点までのones行列を用いhough変換し求めた空間の分布例を示す。

改善前のもの

for i=114:2:130;subplot(3,3,(i-114)/2+1);mesh(hough(ones(i,i),i,i));end

以下の図は、改善した例である。

for i=114:2:130;subplot(3,3,(i-114)/2+1);mesh(houghf(ones(i,i),i,i));end

高速化のためのファインチューニング

スクリプトに比べてかなり高速化できた。細かいことであるが、以下のテクニックを使うと若干ではあるが速度アップに効果がある。例えば、

for(jj = 0;jj < X;jj++) {

    for (ii = 0;ii < Y;ii++) {

     if(im[jj*Y + ii] > 0) {

       iiY_2 = (double)(ii - X_2);

     for(theta = 0;theta < thetamax;theta++) {

        rho = (int)((ii - X_2)* smat[theta] + (jj - X_2) * cmat[theta] + rhomax_2);

        if((rho < 0) || (rho >= rhomax)) continue;

        yy[theta * rhomax + rho] += 1.0;

       }

     }

    }

   }

の処理を以下のように変更するとよい。まず変数jjY,jjX_2,iiY_2を宣言し、同じ計算をしないように出来る限りループの外に追い出して計算している。なおこのテクニックは、若干読みづらくなるがMATLAB、C言語のみならず様々な言語でも応用できるテクニックである。最新のコンパイラでこれらを検出、自動的にサポートしているかもしれないので一応、速度比較してみるとよい。

for(jj = 0;jj < X;jj++) {

    jjY = jj * Y;

    jjX_2 = (double)(jj - X_2);

    for (ii = 0;ii < Y;ii++) {

     if(im[jjY + ii] > 0) {

       iiY_2 = (double)(ii - X_2);

       for(theta = 0;theta < thetamax;theta++) {

        rho = (int)(iiY_2 * smat[theta] + jjX_2 * cmat[theta] + rhomax_2);

        if((rho < 0) || (rho >= rhomax)) continue;

        yy[theta * rhomax + rho] += 1.0;

       }

     }

    }

   }

Sparse行列、Uint8行列への対応

　一般にHough変換は、2値のデータを扱い、値が0の時は演算をせず、特に1の場合にのみ変換を行う。つまり、画像の点が少なければ少ないほど処理時間が速くなる。MATLABで扱う通常の行列は、Full Matrixであり、行列の要素が0でも1でも関係無しにメモリ内に記憶されるため、大きな配列を宣言した場合には、大きなメモリ空間を要求される。特に、行列の内部の値が0でない個所の行と列番号とその値のみを記録するようにすれば、メモリを有効に活用できる。このような発想からMATLABでは、スパース行列というものが定義されている。例えば、1000x1000の単位行列を定義してその容量を見てみると

》 clear all

》 seye=(sparse(eye(1000,1000)));

》 fulleye=eye(1000,1000);

》 whos

  Name          Size         Bytes  Class

  fulleye    1000x1000     8000000  double array

  seye       1000x1000       16004  sparse array

Grand total is 1001000 elements using 8016004 bytes

と8000000byteから16004byteと同じサイズの行列でもかなり異なることがわかる。（このことは、メモリだけでなく処理速度にも関わってくる。そこでSparse行列に対しても同様の演算を行えるようにしたのが以下のスクリプトである。

また、画像処理は、比較的大きな行列を扱うが、行列内の数値は、0ばかりでは無いためsparse行列は使えない。1ドットに対し最大255までの数しか記録できないがその分メモリ消費が8分の1で済むuint8行列というのが定義されている。単色表現は、256階調程度あれば十分であることからdoubleのfull Matrixの代わりにuint8のfull Matrixもよく使われる。ここでは、以上上で述べた成果を含め、FULL行列とSparse行列、uint8行列の3つに対応したルーチンを組み込んである。入力された引数により自動的に判別するようになっており使用法は、MATLABスクリプトによるものと変わりはない。入力がどの場合でも出力は、doubleのfull Matrixになっている。（この点もスクリプトと同じ。）

》ueye=uint8(eye(1000,1000));

》whos

  Name          Size         Bytes  Class

  fulleye    1000x1000     8000000  double array

  seye       1000x1000       16004  sparse array

  ueye       1000x1000     1000000  uint8 array

-----------------------------houghf.cpp hopefully final version-----------------------------------------------------------

#include <stdio.h>

#include <math.h>

#include "mex.h"

/*

function res=hough(im,rhomax,thetamax)

% Name:   hough(im,RHO_MAX,THETA_MAX)

% Version:  v1.0

% Author:   Dimitrios Ioannou

%    dioan@robotsg.nuceng.ufl.edu

%    dioan@alder.circa.ufl.edu

% Date:    08/23/95

% Arguments:

%    im: is the input,binary, image. If the

%    image is not binary pixels having

%    non-zero values are considered.

%    RHO_MAX: is an integer number specifying

%    the rho quantization.

%    THETA_MAX: is an integer number

%    specifying the theta quantization

% Purpose:

%    perform the hough transform of a binary

%    image

% Dependencies:

%    None

% Example:   v=hough(im,256,256)

%    input is the image im, and the

%    quantization is d_rho=X/256 and d_theta=pi/256

%    if the size of the image is 256 by 256

%    d_rho=1.

%

%    v is the number of votes in the

%    paremeter space. v(i,j) is the number

%    of votes for the strip having distance from

%    the center of the image equal to

%    (i-RHO_MAX/2)*d_rho (d_rho=X/RHO_MAX, the

%    image is X by X  pixels),and its normal has

%    angle j*d_theta,(d_theta=pi/THETA_MAX)

%

%    for a 256 by 256 image, the center of the

%    image is the center of the pixel (128,128)

%    i=1 => rho=(i-1-128)*d_rho=-128*d_rho

%    i=256 => rho=(i-1-128)*d_rho=127*d_rho

%    this essentially means that:

%    'the image is not symmetric around its center'.

%

Arranged by Gerox(c) for mex file 1999

Arranged by Gerox(c) for sparse matrix 1999.08.22

Arranged by Gerox(c) for uint8 matrix 1999.08.25

*/

void mexFunction(int nlhs,mxArray *plhs[],int nrhs,const mxArray *prhs[]) {

int i,ii,jj;

int theta,rho;

if ((nrhs != 3) || (nlhs != 1)) {

   mexPrintf("function res=hough(im,RHO_MAX,THETA_MAX)\n");

   mexPrintf("Based on m-script file (Author:Dimitrios Ioannou: hough.m v1.0)\n");

   mexPrintf(" which is available from www.mathworks.com under user contributed library\n");

   mexPrintf("Arranged for MEX version by Gerox(c) Copyright 1999 %s\n",__DATE__);

   mexErrMsgTxt("\n");

}

int rhomax,thetamax,X,Y;

rhomax = (int)mxGetScalar(prhs[1]);

thetamax = (int)mxGetScalar(prhs[2]);

//[M,N]=size(im);

X = (int)mxGetN(prhs[0]);

Y = (int)mxGetM(prhs[0]);

if (X != Y) {

   mexPrintf("Input image is not square. Exiting!\n");

   return;

} else {

   if ((X % 2) == 1) {

    mexPrintf("Input image size has to be even in pixels. Exiting!\n");

    return;

   }

}

double pi = 3.14159265358979;

double *im = mxGetPr(prhs[0]);

// Since we need theta from 0 to pi

// check result of

// mesh(hough(ones(120,120),120,120));

// mesh(houghf(ones(120,120),120,120));

double d_theta = pi / (double)(thetamax - 1);

// theta=0:d_theta:pi-d_theta;

double *smat = (double*)mxCalloc(thetamax,sizeof(double));

double *cmat = (double*)mxCalloc(thetamax,sizeof(double));

double dd_rho = (double)rhomax / (double)X;

double tmp;

for (i = 0,tmp=0.0;i < thetamax;tmp += d_theta,i++) {

   smat[i] = sin(tmp) * dd_rho;

   cmat[i] = cos(tmp) * dd_rho;

}

// [x,y]=find(im);

double rhomax_2 = (double)(rhomax >> 1) + 0.5;

int X_2 = (int)(X >> 1);

plhs[0] = mxCreateDoubleMatrix(rhomax,thetamax,mxREAL);

double *yy = mxGetPr(plhs[0]);

int jjY;

double jjX_2;

double iiY_2;

if(mxIsDouble(prhs[0])) {

   for(jj = 0;jj < X;jj++) {

    jjY = jj * Y;

    jjX_2 = (double)(jj - X_2);

    for (ii = 0;ii < Y;ii++) {

     if(im[jjY + ii] > 0) {

       iiY_2 = (double)(ii - X_2);

       for(theta = 0;theta < thetamax;theta++) {

        rho = (int)(iiY_2 * smat[theta] + jjX_2 * cmat[theta] + rhomax_2);

        if((rho < 0) || (rho >= rhomax)) continue;

        yy[theta * rhomax + rho] += 1.0;

       }

     }

    }

   }

} else {

   if(mxIsSparse(prhs[0])) {

//   [x,y]=find(im);

    int *ir = mxGetIr(prhs[0]);

    int *jc = mxGetJc(prhs[0]);

    for (int col = 0;col < X;col++)  {

     int start = jc[col];

     int stop = jc[col+1];

     if (start == stop) continue;

     jjX_2 = (double)(col - X_2);

     for (int cnt = start; cnt < stop; cnt++)  {

//      mexPrintf("\t(%d,%d) = %g\n", ir[cnt]+1, col+1, data[total++]);

       iiY_2 = (double)(ir[cnt] - X_2);

       for(theta = 0;theta < thetamax;theta++) {

        rho = (int)(iiY_2 * smat[theta] + jjX_2 * cmat[theta] + rhomax_2);

        if((rho < 0) || (rho >= rhomax)) continue;

        yy[theta * rhomax + rho] += 1.0;

       }

     }

    }

   } else {

    unsigned char *imi = (unsigned char*)mxGetPr(prhs[0]);

    if(mxIsUint8(prhs[0])) {

     for(jj = 0;jj < X;jj++) {

       jjY = jj * Y;

       jjX_2 = (double)(jj - X_2);

       for (ii = 0;ii < Y;ii++) {

        if(imi[jjY + ii] > 0) {

         iiY_2 = (double)(ii - X_2);

         for(theta = 0;theta < thetamax;theta++) {

           rho = (int)(iiY_2 * smat[theta] + jjX_2 * cmat[theta] + rhomax_2);

           if((rho < 0) || (rho >= rhomax)) continue;

           yy[theta * rhomax + rho] += 1.0;

         }

        }

       }

     }

    } else {

     mxFree(smat);

     mxFree(cmat);

     mexErrMsgTxt("Input must be double or sparse or uint8 Matrix");

    }

   }

}

mxFree(smat);

mxFree(cmat);

}

演習問題

4.1 直線パラメータを求めるhough変換において、円、正三角形、長方形、正方形はrho,theta空間でどのような形に変換されるのか？説明せよ。回転,直進移動,拡大、縮小させたときは？

4.2 スキャナーなどで写真をスキャンする場合、上手くスキャンする対象を置かないとx−y軸が傾いてスキャンされてしまう。hough変換を用い傾き角度を検出、自動補正するスクリプトを書け。

4.3 円の大きさを10に固定し自由度2の円のパラメータを求めるhough変換プログラムをスクリプトにより書け。

4.4 4.3で作ったスクリプトをC言語に変換せよ。また、どの程度高速化できたかを検討せよ。