MATLABでの座標系について

MATLABでは、実は、グラフ、グラックス、行列と様々な概念を取り入れ座標系を定義している。それぞれ従来の慣習にならい座標系を定義しているため混乱してしまいがちである。ここでは、これらいくつかの座標系を実例を交えながら解説していく。

MATLABで使用される座標系は、

直交座標系

行列座標系

ピクセル座標系

の3つがある。

1.直交座標系(Cartesian coordinate system)は、この座標系は、plot,plot3などに使用される座標系でもっとも一般的な座標系である。この系では、最初の成分xは、右方向へ増加し、2番目の成分yは上方向に増加する。原点(0,0)は、下左隅である。

例えば、(2,3)-(4,1)の点を描いてみると

plot(2,3,'p',4,1,'x');axis([0 5 0 5]);xlabel('x');ylabel('y')

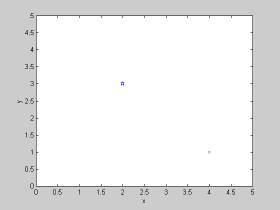
行列座標系

行列座標系(row-column coordinate system)は、MATLABの行列が元来FORTRAN言語のそれから発展した経緯から由来する。行列座標系では、最初の成分i(行row)yは下方向に増加し、2番目の成分j(列col)xは、右方向に増加する。原点は、行列と同様に左上隅である。

(1,1) (1,2) (1,3) (1,4) (1,5)

(2,1) (2,2) (2,3) (2,4) (2,5)

(3,1) (3,2) (3,3) (3,4) (3,5)

(4,1) (4,2) (4,3) (4,4) (4,5)

(5,1) (5,2) (5,3) (5,4) (5,5)

行列に対応する(2,3),(4,1)を1にしてグラフ化してみよう。

[0 0 0 0 0;...

0 0 1 0 0;...

0 0 0 0 0;...

1 0 0 0 0;...

0 0 0 0 0];

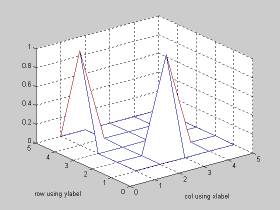
mesh([0 0 0 0 0;0 0 1 0 0;0 0 0 0 0;1 0 0 0 0;0 0 0 0 0]);axis([0 5 0 5 0 1]);

xlabel('col using xlabel'); ylabel('row using ylabel')

　

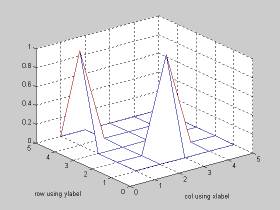
となる。

ピクセル座標系

ピクセル座標系(pixel coordinate system)は、ディジタルイメージプロセッシングに使用される一般的な座標系である。これは、画面の左上隅が原点となり最初のx成分が右方向に増加し、y成分が下方向に増加する座標系である。先ほどの行列をイメージで表示すると

image([0 0 0 0 0;0 0 1 0 0;0 0 0 0 0;1 0 0 0 0;0 0 0 0 0]*255);

xlabel('col using xlabel'); ylabel('row using ylabel');

 

 

 

 

 

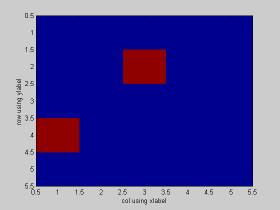
ここで注意比較してもらいたいのが表示される点の位置である。

　

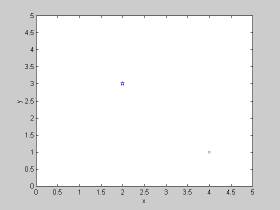
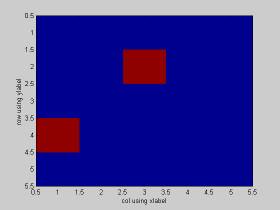
ここで注意してもらいたいのは、これらのデータはそれぞれ一般的な座標表現で(2,3),(4,1)の点を表示する命令である。しかし図を見てわかるようにそれぞれ座標系によりx-y座標の原点の違い、軸の定義の違いなどによりことなるので扱う場合には、注意する必要がある。

特に注意しなければならないのがオーバーラップ表示したときである。同じ点を指しているつもりでも

image([0 0 0 0 0;0 0 1 0 0;0 0 0 0 0;1 0 0 0 0;0 0 0 0 0]*255);

xlabel('col using xlabel'); ylabel('row using ylabel');

hold on

plot(2,3,'pw',4,1,'xw');axis([0 5 0 5]);xlabel('x');ylabel('y')

hold off

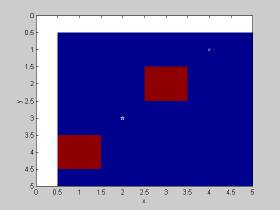
とこのように軸が逆になってしまっていることがわかる。

mesh([0 0 0 0 0;0 0 1 0 0;0 0 0 0 0;1 0 0 0 0;0 0 0 0 0]);axis([0 5 0 5 0 1]);

xlabel('col using xlabel'); ylabel('row using ylabel')

hold on

plot3(2,3,1,'p',4,1,1,'x');axis([0 5 0 5 0 1]);xlabel('x');ylabel('y')

hold off

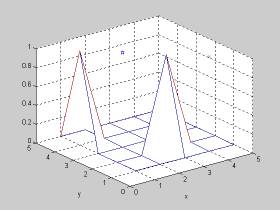
の場合も同様である。

 

 

まとめると以下のようになる。

Cartesian coordinate system	行列のインデックスをx-y座標と考えた場合には、軸が逆になる。
row-column coordinate system	row-i-y col-j-xの対応になる。
pixel coordinate system	y軸の順が逆になる。