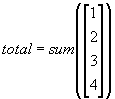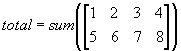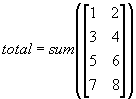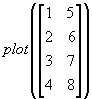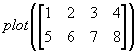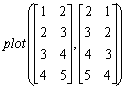MATLAB関数でのベクトルや行列の扱い........................................................................ 37
SUM関数..................................................................................................................... 37
RESHAPE関数............................................................................................................ 38
MATLABの座標系による行列データの扱いの違い.......................................................... 38
PLOT関数.................................................................................................................... 38
y軸のみの場合。...................................................................................................... 39
x軸y軸を指定した場合。........................................................................................ 39
MESH,SURF,WATERFALL関数................................................................................. 40
IMAGE関数................................................................................................................. 41
FIND関数.................................................................................................................... 41
FINDSTR関数............................................................................................................. 42
MATLAB関数による効果的な応用プログラミング例...................................................... 43
2次元行列の中でもっとも大きい値の行列の座標を求めるには？................................ 43
解答1........................................................................................................................ 43
解答2........................................................................................................................ 43
解答3........................................................................................................................ 44
解答4........................................................................................................................ 45
処理速度による解答1から4の比較............................................................................. 45
演習問題........................................................................................................................... 47
MATLAB関数でのベクトルや行列の扱い
MATLABは行列をベースに開発された言語である。ベクトルや行列をフルに活用すると簡潔にわかりやすくかつ処理速度も速くなるようにインプリメントできる。ここでは、いくつかのMATLAB関数について一般的な使用法、それにMATLAB特有の使用法について例を挙げながら見てみよう。
SUM関数
この関数では、アレイデータの合計を求めるときに使用する。C＋＋言語で実現するには、以下のように記述できる。
double sum(double *data,datnum) { // C言語の場合、データ配列はポインタで渡すので
double total=0; //全体の個数はわからない。
for (int i = 0;i < datnum;i++) { //そこで引数で大きさを渡す必要がある。
total += data[i];
}
return total;
}
MATLABでSUM関数と等価のスクリプトを書くと以下のようになる。
function total=orginalsum(data) %MATLABの場合には、データ数を入れる必要はない。
total=0; % この場合、保存するファイル名は、originalsum.mとして保存する。
for i=1:length(data)
total = total + data(i);
end
標準的な使用法のSUM関数は、たった5行のスクリプトで記述できる。ちなみにSUM関数を使って書くと、total=sum(data);と表現できる。MATLABで用意されているSUM関数は、スクリプトに比較すると数倍処理速度が速くなるようにインプリメントされている。またMATLABのSUM関数では、以下の表のように1次元アレイを扱うのみでなく行列でも計算できるように拡張されている。
|
タイプ |
書き方の例 |
結果 |
SUMの方向 |
|
|
|
10 |
行向き |
|
|
10 |
列向き |
|
|
|
|
[6 8 10 12] |
列向き |
|
|
[16 20] |
列向き |
アレイの場合には、列アレイでも行アレイでも同様にアレイとして計算する。しかし、入力が行列になった場合には、列方向にのみ作用する。したがって、SUM関数を使いアレイを行列化し一気に計算する場合には、行列の向きを注意する必要がある。SUM関数の場合には、一応、行方向に演算したい場合などには、sum(data,2)のように2番目の引数に2を設定することで行方向に設定することも可能になっている。（入力する行列を転置すれば済む話であるが・・・）このような拡張は、SUM関数のみでなくMATLABに標準でインプリメントされている様々な関数に対しても拡張がなされている。直感的に大体の振る舞いは、類推できるが関数の機能が違うため当然オプションも異なる場合もあるのでので詳しい使用法やオプションに関しては、help 関数により調べるとよい。
RESHAPE関数
この関数は、行列の行と列のサイズを変更する関数である。MEX関数のところでも扱うが、この関数を使用する場合に注意しなければならない点がある。それは、
通常、C言語などで2次元配列を作った場合には行列の要素は、
1,2,3,4,5,6,...と言う行形式順序で記録されている。しかしMATLABは、元来FORTRAN言語の仕様から内部配列の格納法が定義されたため格納法が異なる。MATLABでは、1,2,3,4,...の順で格納された3x3の行列はMATLAB内部では、
という列形式になっている。特にreshape関数を使うときは、この点を考慮する必要がある。
例えば、C 言語の配列の感覚で3x3の行列
を1x9のアレイに変換してしまうと、reshape([1 2 3;4 5 6;7 8 9],1,9)
ans =
1 4 7 2 5 8 3 6 9
このような結果になってしまう。もしC言語と同様に扱いたい場合には、reshapeする前に転置'をする必要がある。
》 reshape([1 2 3;4 5 6;7 8 9]',1,9)
ans =
1 2 3 4 5 6 7 8 9
MATLABの座標系による行列データの扱いの違い
MATLABでは、画像処理、3次元表示、行列データ表示などを行うため、複数の座標系を定義し使われている。ここでは、mesh関数に代表される3次元表示関数、image関数,xy座標で表示するplot関数を例に行列データの扱いについて説明する。
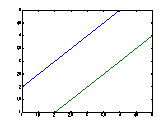
PLOT関数
この関数は、xy座標データを表示するもっともポピュラーな関数である。plot関数で表示されるグラフの軸は、上向きがy軸で正の方向、右横向きがx軸で正の方向になっている。
この関数もアレイデータと行列データでは、x軸の大きさとy軸行列の大きさにより自動的に決まる。
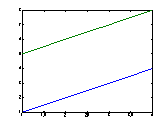
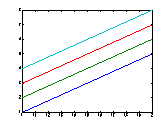
y軸のみの場合。
|
タイプ |
書き方の例 |
結果 |
データ方向 |
|
アレイ |
plot([1 2 3 4]) plot([1 2 3 4]') |
|
自動判別 行アレイ、列アレイどちらでも同じ |
|
|
plot([1:4;5:8]')
|
|
列向き |
|
plot([1:4;5:8])
|
|
x軸y軸を指定した場合。
|
タイプ |
書き方の例 |
結果 |
データ方向 |
|
アレイ |
plot([1 2 3 4],[1 2 3 4]) plot([1;2;3;4],[1 2 3 4]) plot([1;2;3;4],[1;2;3;4]) plot([1 2 3 4],[1;2;3;4]) |
|
自動判別 行アレイ、列アレイどちらでも同じ |
|
x軸がアレイ y軸が行列 |
plot(1:4,[1:4;5:8]) plot(1:4,[1:4;5:8]') plot(1:4',[1:4;5:8]') |
|
x軸アレイの大きさに合わせる。もしxyの長さが同じ場合には、x軸アレイの向きに依存 |
|
plot(1:2',[1:4;5:8]) plot(1:2,[1:4;5:8]) plot(1:2',[1:4;5:8]') |
|
||
|
|
plot([1:4;2:5],[2:5;1:4])
|
|
列向きでそれぞれの列が対応 |
|
plot([1:4;2:5]',[2:5;1:4]) plot([1:4;2:5],[2:5;1:4]') |
エラー |
サポートせず |
|
|
plot([1:4;2:5]',[2:5;1:4]')
|
|
列向きでそれぞれの列が対応 |
また、プロットでは、plot(xdata,ydata,'c+:')などのように表示するデータの色や形や線種などの指定も出来る。plot(xdata1,ydata1,xdata2,ydata2)と言ったように複数のデータもオーバーラップして表示することも可能である。ただしplotでとることの出来る引数は50までであるのでそれ以上の線をひく場合には、テクニックが必要になる。（x軸y軸データを行列化したり、hold関数で更に新しいプロットを使うなど）plot関数のオプション等は、helpで調べられるのでそれで確認すればよい。
MESH,SURF,WATERFALL関数
mesh,surf,waterfall（これらの関数の使用引数は同じ若干表示画面が異なる）など2入力1出力データを表示する関数もその表示の向きについて調べてみよう。
》 data=[1 2 3;4 5 6;7 8 9]
data =
1 2 3
4 5 6
7 8 9
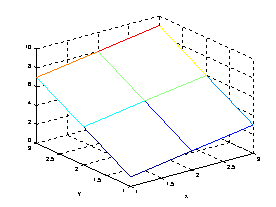
このような変数データをmesh関数で表示すると以下のようになる。
》 mesh(data)
》 ylabel('y')
》 xlabel('x')
4 3 2 1 9 8 7 5 6
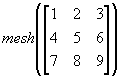
IMAGE関数
この関数は、画像を表示する関数であるが、上で説明したMESH関数などとは表示座標系が異なるので注意すること。イメージの場合、y座標の向きが上下逆になる。
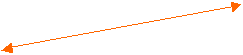
data(:,:,1)=[1 2 3;4 5 6;7 8 9]/9;
data(:,:,2)=[1 2 3;4 5 6;7 8 9]/9; % R,G,Bカラーを全て同じ値にして
data(:,:,3)=[1 2 3;4 5 6;7 8 9]/9;%白黒の濃淡データを作成
image(data);%0に近いほど黒へ1 に近いほど白くなる。
ここでは、引数がdoubleの場合、0 〜1までの値にする必要があるため９で割っている。 9 8 7 6 5 4 3 2 1
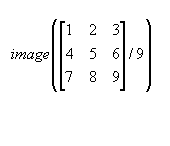
MATLABには、プロット座標系、イメージ座標系、行列座標系がありそれぞれ軸が異なるので使用するときには、注意を要する。（実は、詳しく言うと3次元プロットの座標系、極座標などなどもっと種類はあるがここでは扱わない。）
FIND関数
FIND関数は、0でない行列、アレイの位置を取り出してくれる関数である。処理によっては、この関数や、SORT関数などを駆使すると、処理時間のかかるfor文などがほとんどいらなくなる。また、論理関係演算子(<,>,<=,>=,==,~=)などを使用すれば特定のパターンの抽出もできる。
例えば、3x3の単位行列eye(3,3)から、1である行と列の番地を取り出すには、
》 [row,col]=find(eye(3,3)==1)
row =
1
2
3
col =
1
2
3
とすればできる。また、FIND関数とMAX関数と併用すれば最大値の位置とその大きさの検出などができる。
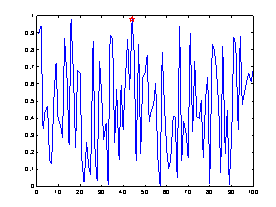
data=rand(1,100);i=find(data==max(data));
plot(1:length(data),data,i,data(i),'rp','markersize',10);
まず、max(data)でデータの最大値を取り出している。その後
data==max(data)とすると、dataと同じ大きさでmax(data)と同じ値の個所だけ1で他は0となる1次元アレイが出来る。find関数は0でない個所を探すので1となったmax(data)の位置がFIND関数の出力になる。
FINDSTR関数
FINDSTR関数は、名前からすると文字列データの中の特定の文字パターンの検出に使用する関数として作られたようである。これを応用すると、ある時系列データの特別なパターンの検出にも使用できる。例えば、データの中で凸の位置の検出を考えてみよう。
》 data=sin(0.1*(1:100));
サイン波のデータを考える。通常、ピークを求めるのであれば、範囲を決めてMAX関数を使えばよいが、周期的な波形での凸位置検出するための範囲設定などする必要があり余り適当であるとは言えない。そこで、凸を検出するため、微分による方法を示す。DIFF関数によりdataアレイを微分する。凸の検出には、符号が重要なのでSIGN関数により±1の時系列データに変換する。なお、この際、DIFF関数で処理したデータ長は、微分操作を行うため、1つ分データ長が短くなるのでplotする場合、diff(data)のデータ数は、length(data)-1になるので注意すること。
》 plot(1:length(data),data,1:length(sign(diff(data))),sign(diff(data)))
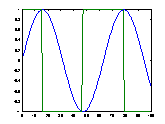
変換したデータを用いFINDSTR関数と凸になる[1 -1]と変化する個所を検出している。
》 i=findstr(sign(diff(data)),[1 -1])
i = 15 78
》 plot(1:length(data),data,i,data(i),'rx','markersize',10)
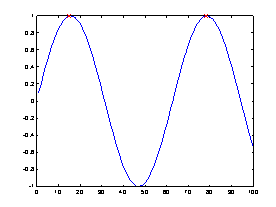
このようにピーク値のみの検出が可能になる。例えば、ノイズなどの影響を防ぎたい場合などには、[1 -1]でなく[1 1 -1 -1]など検出条件を厳しくすることもできる。ただし検出する位置は、検出先頭アドレスになるので注意すること。
MATLAB関数による効果的な応用プログラミング例
2次元行列の中でもっとも大きい値の行列の座標を求めるには？
例えばpeaks関数を用い2次元配列をつくりそのデータをもとに考えてみよう。
まず、peaks関数を使い2次元データaを作る。
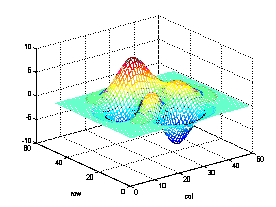
a=peaks;
mesh(a);xlabel('col');ylabel('row');
ここで表示された行列データaからピーク値を検出するにはどうしたら良いであろうか？
解答1
最大値を求めるには、配列、スカラーを扱う一般的な言語の定石で計算法をMATLABで素直にインプリメントすると以下のようになる。
rownum = 1;colnum = 1;maxval=a(1,1);%Initial Condition for maxval
[row,col]=size(a);
for cntrow=1:row
for cntcol=1:col
if (a(cntrow,cntcol) > maxval)
maxval = a(cntrow,cntcol);
rownum = cntrow;
colnum = cntcol;
end
end
end
実は、このインプリメンテーションでの処理速度は非常に遅い。実際、C言語などからMATLABを使うようになった人は、この動作速度からMATLABは非常に実行が遅いなどと結論をだしてしまいがちである。（実は、私もそうであった。）しかし、MATLABはコツをつかみ上手くプログラミングすると下手なC言語プログラミングより可読性が高くかつ高速処理可能なプログラミングができる。そのコツと言うのが、ベクトル処理化である。MATLABは行列演算を得意とする。比較をする場合でもベクトル演算できる関数を使用し極力for文を省きベクトルのまま処理をすれば、大幅な処理速度アップが期待できる。上の例の計算では、最大値を調べるのにfor文を使いデータを1つ１つ比較している。これが遅くなる原因である。
解答2
MATLABにはfind関数という関数がある。元来この関数は、行列の中の0以外の要素を取り出す関数である。もしfind(max(max(a))==a)とすれば、max(max(a))で得られた値と一致するa行列の中のrow,col座標を取り出すことも出来る。つまりこのfind関数を応用すると実は、
[rownum,colnum,maxval]=find(max(max(a))==a);
とたった1行で記述できてしまうのである。これでも処理速度の改善には十分であるのだが、もうちょっと頭を働かせてみよう。find関数は、汎用的な処理をする関数でありいくら最適化してあると言っても若干の処理時間がかかる。またこの中では、MAX関数も2回呼び出している。そこでまず、1つのアプローチとしてfind関数を使わない方法を考えてみよう。
解答3
MATLABのMAX関数は、データが行列ならば、MAX関数は、各列の最大要素を含む行ベクトルを出力する。そこで2次元データのx,y座標を求めるためには、max関数一回では求めることはできない。
[maxvec,rowvec]=max(a);
[row,col]=size(a);
hold on
plot3(1:col,rowvec,maxvec,'x','linewidth',5)
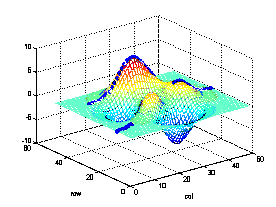
x印のついているところがmaxで求められたベクトルmaxvec,rowvecである。
次にこの求められたベクトルmaxvecの中からまた最大値をmax関数により探せばよい。
[maxval,colnum]=max(maxvec);
maxvecは、アレイなので2次元の中の最大値maxvalそれにその位置は、列については、colnum,行については、rowvecアレイの中のcolnum番目の値つまりrowvec(colnum)で求めることが出来る。よってプロットすると
plot3(colnum,rowvec(colnum),maxval,'rp','markersize',20);
hold off
となる。
求められた最大値は、maxval =8.0752,row=38,col=25である。
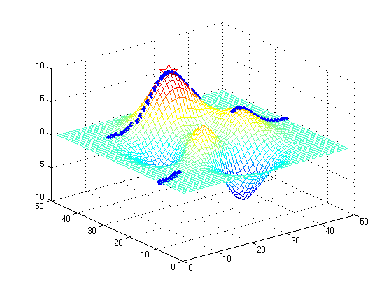
解答4
また、高速化の手段としてMAX関数を2回呼ばない方法も考えられる。このトリックは、reshape関数により行列をアレイに変換する手法である。まず、
[row,col]=size(a);
[val,num]=max(reshape(a,1,row*col));
とする。reshapeした配列でMAX関数を使い最大値を求める。その中から行と列のサイズを取り出す。今ここで、numとrow,colとの関係は、num= rownum +colnum*rowの関係になる。(この際、C言語では、colとrowの順が逆なので注意すること！)そこでこの関係式からcolnum,rownumを求めたい。MATLABでは、C言語で割り算の余りを計算する演算子%と同様の機能の関数としてrem関数がある。まずこの関数を用いrownumは、num÷row=colnum余りrownumなのでまずrem関数により余りを計算する。
rownum=rem(num,row);
次にその行の数をひいた後、行数で割る。MATLABの行列は1から始まるのでその数に1を足したものが列数になる。
colnum=(num-rownum)/row+1;
[rownum,colnum,a(rownum,colnum),toc]
これで完成である。
ここでは、2次元データの最大値とその場所を求めるための方法を４つ考えてみた。MATLABでは、ベクトル演算を上手く活用することでかなりの処理速度が改善できる。
Tips:
-----------------------------------------------------------------------------------------------------
ちなみにMATLABでは、サイズを得るときには、
[row,col]=size(a);
と行(row),列(col)の順序で値を得るのに対し、3次元プロットを呼ぶ際には、
plot3(colnum,rowvec(colnum),maxval,'rp','markersize',20);
列(col),行(row),その大きさという順で扱うので注意すること！！
-----------------------------------------------------------------------------------------------------
処理速度による解答1から4の比較
以上のスクリプトをまとめて書き、コンピュータで実行、比較した。ここでは、処理時間の違いをより明らかにするために、peaks関数によるデータ生成は、500x500のサイズデータを用いている。
% Filename spdtest.m Gerox(c) 1999
% 解答１
clear all
a=peaks(500);
tic;
rownum = 1;
colnum = 1;
maxval=a(1,1);
[row,col]=size(a);
for cntrow=1:row
for cntcol=1:col
if (a(cntrow,cntcol) > maxval)
maxval = a(cntrow,cntcol);
rownum = cntrow;
colnum = cntcol;
end
end
end
[rownum,colnum,maxval,toc]
%解答2
clear all
a=peaks(500);
tic;
[rownum,colnum,maxval]=find(max(max(a))==a);
[rownum,colnum,a(rownum,colnum),toc]
%解答３
clear all
a=peaks(500);
tic;
[maxvec,rowvec]=max(a);
[maxval,colnum]=max(maxvec);
[rowvec(colnum),colnum,maxval,toc]
%解答４
clear all
a=peaks(500);
tic;
[row,col]=size(a);
[val,num]=max(reshape(a,1,row*col));
rownum=rem(num,row);
colnum=(num-rownum)/row+1;
[rownum,colnum,a(rownum,colnum),toc]
PentiumII 350MHzマシンでは、
》 spdtest
ans = 382.0000 250.0000 8.1061 3.0200
ans = 382.0000 250.0000 8.1061 0.1700
ans = 382.0000 250.0000 8.1061 0.0600
ans = 382.0000 250.0000 8.1061 0.0600
》
となった、最後にかかれている数字は処理に要した時間である。100分の1秒単位までカウントする関数tic/tocのコンビネーションで計測した。解答1のCの定石の方法では、3.02秒かかっている。解答2の1行で記述可能なfind関数とmax関数の組み合わせでは、0.17秒と非常に高速化できている。さらに解答3のmax関数のみを用いベクトル計算をフルに活用した例と解答4のreshape関数とmax関数を1つだけ活用した例は、同時間の0.06秒とさらに高速化できていることがわかる。
MEX関数の章で扱うが、MATLABでは、処理速度がどうしても遅いときなどには、MEX関数を用いてC言語で記述する方法もある。しかしスクリプトの書き方次第でも3.02/0.06=約50倍の差がでた。このようにベクトルを駆使すれば、かなりの高速化が期待できる。
演習問題
2.1 2次元行列データa=peaks;の中で凸となる個所のx,y座標を見つけ出せ。
for文を用いたスクリプトとMATLAB関数を最大限に活用したスクリプトの速さを比
較せよ。
2.2 見つけ出した凸となった個所に☆マークを表示せよ。
2.3 乱数data=rand(1,100);で作ったデータから上位5点の大きさとその位置を見つけ出
せ。
2.4 見つけ出した点とdataをオーバーラップして表示せよ。
a=peaks;
tic;
rownum=1;colnum=1;maxval=a(1,1);
[row,col]=size(a);
txy=[];
for cntrow=2:row-1
for cntcol=2:col-1
pflag=[ a(cntrow,cntcol)-a(cntrow-1,cntcol-1);...
a(cntrow,cntcol)-a(cntrow-1,cntcol) ;...
a(cntrow,cntcol)-a(cntrow,cntcol-1) ;...
a(cntrow,cntcol)-a(cntrow+1,cntcol-1)];
mflag=[ a(cntrow+1,cntcol+1)-a(cntrow,cntcol);...
a(cntrow+1,cntcol)-a(cntrow,cntcol);...
a(cntrow,cntcol+1)-a(cntrow,cntcol);...
a(cntrow-1,cntcol+1)-a(cntrow,cntcol)];
if(pflag > zeros(4,1) & mflag < zeros(4,1))
txy=[txy; cntrow cntcol];
end
end
end
txy
toc
mesh(a)
hold on
i=length(txy);
for j=1:i
plot3(txy(j,2),txy(j,1),a(txy(j,1),txy(j,2)),'rp')
end
hold off
clear
I=peaks;
tic
DY=(I(2:end-1,1:end-2)<I(2:end-1,2:end-1)).*(I(2:end-1,2:end-1)>I(2:end-1,3:end));
DX=(I(1:end-2,2:end-1)<I(2:end-1,2:end-1)).*(I(2:end-1,2:end-1)>I(3:end,2:end-1));
mesh(DX.*DY)
[i,j]=find(DX.*DY>0.5)
k= sum(I(i+1,j+1).*eye(length(i)));
mesh(I);hold on;plot3(j+1,i+1,k,'p');hold off;
toc