p.141 直交関数の内積(2007.03.07)
p.141
誤:「直交関数とは、周期Pの信号で積分すると0になるような関数のことである」
正:「2つの関数bi, bjは、その内積が0であるとき直交するという。また、関数列b1, b2, ..., bnが与えられたとき、異なる2つの関数がすべて直交している場合その関数列を直交関数列という。」
再々訂正ということで、ご迷惑をかけて申し訳ありませんでした。
p52の比較演算子の表(2006年11月16日)
記号:<
式:A
p.193 arfftcomp.m の追加事項です。(2006年11月11日)
自己回帰モデルでは、差分方程式のパラメータを求めています。このパラメータのままでは、サンプリング時間に依存しないため連続系に変換する処理を行うため、 d2cm関数を用いています。c2dm関数により連続系のパラメータに変換後、bode関数によりボード線図の表示を行っています。ちなみに、自己回帰モデルの方程式は、下記のようになるので、
この式をシフト演算子
このように変換し、伝達関数を求めると
となります。ここで、シフト演算子
を計算すれば、周波数特性を見ることができます。
これらを用い、コントロールツールボックスの c2dm関数、tf関数、bode関数を使わずに実現するには、
|
[num,den]=d2cm(1,dend,dt); |
|
ff=(0:dt/10:f(len2)); |
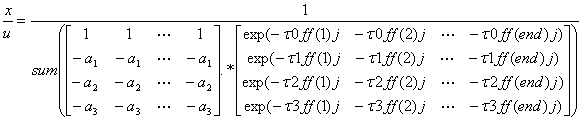
のようになります。sum関数は、縦方向に足し算をするため、この計算により周波数ffの間の値を1行の式ですべて計算することができます。 なお、位相特性については、簡易法を用いているため、bode関数のそれとは、離散系から連続系への変換の近似アルゴリズムの違いにより若干結果が異なります。
http://www.ikko.k.hosei.ac.jp/~matlab/MATLAB_Handbook2nd.lzh
も更新しました。
最新版 MATLABハンドブック 改定第二版 2006.8.30
p.159
正:
実際に動くスクリプトの方は、乗算になっていましたが、このサンプルスクリプトの例のみ割り算になっていました。単なる誤字です。
申し訳ありません。
P.61
誤:fileread.m
正:fileread2.m
テキストファイルを読み込むスクリプトがが既存のMATLAB M関数とバッティングするとの指摘がありました。
このmファイルがカレントディレクトリある場合、GUI操作による文字列を含むテキスト
データのインポートができなくなるそうです。
気づかないで安易な名前をつけてしまいもうしわけありませんでした。
一応、ソースコードの中のファイル名をfileread.m→fileread2.m
に変更いたしました。
もし、カレントディレクトリにfileread.mスクリプトがある場合には、ファイル名を変更
するか削除するようにしてください。
2004.10.14:p.50 の演算子の説明での行列の式の図ですが、
誤:|1 2 3| |x1| |366|
|4 5 6|・ |x2|=|804|
|7 8 9| |x3| |351|
正:|1 2 3| |x1| |366|
|4 5 6|・ |x2|=|804|
|7 8 0| |x3| |351|
の誤りです。見落としておりました。申し訳ありません。
2004.09.15:コンボリューションと内積を混同して記述おりましたp.141の説明では、コンボリューションというより内積(2信号の相関)の方が正解です。混乱させて申し訳ありませんでした。
なお、コンボリューションについての適切な(?)説明は、
http://www.ikko.k.hosei.ac.jp/%7ematlab/xcorr.pdf
に掲載してありますのであわせてご覧ください。
ホントに申し訳ありませんでした。
p.141
誤:コンボリューション
正:直交関数の内積(2信号の相関)
では、なぜ一見複雑に見える信号から、複数の基本的な波形に分解できるのであろうか?
ここで重要な考え方が直交関数である。「直交関数とは、周期Pの信号で積分すると0になるような関数」のことである。
つまり、
式
このような関数bi(t),bj(t)である。
誤:またこの積分のことを畳み込み積分(コンボリューション)と呼ぶ。
正:削除
誤:のコンボリューション
正:削除
は、信号の分解、合成などが可能なため、データ圧縮、画像圧縮などの応用可能である。
sin,cos波の
誤:コンボリューションでは、・・・
正:積分では、・・・・
p.144 の数式
誤:
ω_0=2π/Pとしたとき
∫^2π_0 1・sin(ω・t)dt = 0
∫^2π_0 1・cos(ω・t)dt = 0
∫^2π_0 cos(n・ω・t)cos(m・ω・t)dt = 0 m!=n
∫^2π_0 sin(n・ω・t)cos(m・ω・t)dt = 0 m!=n
∫^2π_0 cos(ω・t)^2dt = P/2
∫^2π_0 1^2dt = P
正:
ω_0=2π/Pとしたとき
∫^P_0 1・sin(n・ω_0・t)dt = 0
∫^P_0 1・cos(n・ω_0・t)dt = 0
∫^P_0 cos(n・ω_0・t)cos(m・ω_0・t)dt = 0 m≠n
∫^P_0 sin(n・ω_0・t)cos(m・ω_0・t)dt = 0 m≠n
∫^P_0 cos(n・ω_0・t)^2dt = P/2
∫^P_0 1^2dt = P
p.143 説明の訂正
データ数/2やデータ数で割る話は、p.154にも書いてあるので、p.143の説明は、
あくまで、sin,cosの直交性だけした方が混乱がないと思いますので以下のように
訂正いたします。
旧:
sin,cos波の積分では、直流成分とナイキスト周波数の間の周波数では、ピークの大きさデータ数/2で割るとその振幅になるのに対し、直流では、データ数で割ることになるので注意すること。
新:
ウォルッシュ変換の場合、どのような(この場合4パターン)の波形の場合でも有限値で割れば信号成分の大きさを復元できる。しかし、sin,cos波を乗算して積分する場合には、一致した特定の周波数で乗算し積分する場合と、(全てが1となるような)直流成分を乗算し積分する場合、有限値の値が異なるので注意すること。